
本文内容来源于《测绘学报》2022年第6期(审图号GS京(2022)0149号)
LI Bofeng, CHEN Guang'e. Precise cooperative positioning for vehicles with GNSS and INS integration[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(8): 1708-1716. DOI: 10.11947/j.AGCS.2022.20210471
高精度导航定位技术推动了时空信息赋能行业的迅猛发展,支撑无人驾驶[1]、智能交通[2]、智慧农业[3]等领域的深度应用。GNSS/INS组合导航综合利用了导航卫星的测距信号和IMU的角速度和比力观测值,实现二者优势互补,有效提升了定位定姿的精度和可用性,已被广泛应用于自动驾驶等领域。然而在复杂的城市环境下,GNSS信号被长时间干扰或遮挡时,组合系统将缺少足够的外部高精度观测值来抑制INS误差,进而造成组合定位发散而无法确保高精度定位的连续性。
针对复杂环境下GNSS/INS组合定位发散的问题,诸多学者开展了相关研究工作并发表了一系列论著。这些方法从本质上可分为两类:一类是通过引入外部其他观测信息来改善定位效果,比如引入车辆自身运动信息[4-5]、加入其他传感器辅助等[6-7];另一类方法是在不增加外部传感器信息的情况下,通过共享车辆之间及车辆与道路之间的信息来实现车辆的协同定位[8]。目前主流的协同定位技术包括协同地图匹配技术(cooperative map matching, CMM)和车辆协同相对位置约束技术(vehicles cooperative relative position constant, VCRPC)。CMM技术基于一定区域内车辆受到的定位误差相似及车辆始终位于道路上这两个基本假设,通过共享此区域内所有车辆的道路约束信息,求解并修正该定位误差,从而提升所有车辆的定位精度[9]。为了提高未参与CMM的车辆的定位精度,文献[10]提出了基于CMM和动对动RTK的协同定位技术,扩宽了常规CMM技术的应用范围。在前人的基础上,文献[11]定性研究了道路约束对CMM精度的影响,为车辆协同网络的设计与优化提供了参考。显然,CMM方法仅适用于对定位精度要求不高的场景,无法满足自动驾驶等场景的高精度定位需求。在VCRPC相关研究方面,文献[12]利用专用短程通信技术(dedicated short-range communication, DSRC)在协同车辆定位方面开展了大量的研究工作,最早提出基于载波频偏的DSRC定位解算方法,建立车辆间的相对空间关系,从而有效提升车辆在弱GNSS信号场景中的定位表现[12]。文献[13]利用激光雷达点云匹配的方式,获取车辆间的相对位置关系,从而实现车辆间观测值的共享,试验结果证明该方法可以有效提高车辆在复杂环境中的定位性能[13]。VCRPC通过整体构建车辆自身及车辆之间的观测模型,建立车辆间待估参数的相对关系,实现车辆间观测值的共享,理论模型严密,是实现协同精密定位的关键。
本文提出一种基于GNSS和INS组合的车辆协同定位技术。首先建立单车GNSS/INS组合定位模型,在此基础上建立了GNSS/INS组合传感器的多车协同定位模型,并给出了相应的解算方法。通过搭建双车试验场景,测试分析了本文方法的效果,为协同精密定位的发展提供参考。便于下文表述简洁,BeiDou/GPS/Galileo/QZSS分别简记为C/G/E/J,北-东-地坐标系(North-East-Down)记为N-E-D;i、e、b和n分别表示惯性系、地心地固系、IMU测量坐标系和当地导航坐标系;en表示元素全为1的n维列向量,In表示n维单位阵;E、D和⊗分别表示期望、方差和克罗内克积算子。
1.1 单车GNSS/INS紧组合定位数学模型
给定载体初始姿态、速度和位置,通过对IMU的角速度和比力观测量积分实现姿态、速度和位置信息的更新。e系下的INS递推公式为[4, 13]
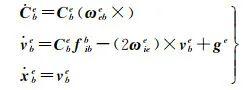 (1)
(1)
式中,f、g、v和x分别表示比力测量值、重力及IMU中心点的速度和位置;(×)代表两个向量间的叉乘算子或单个向量的反对称阵算子[14];(·)为微分算子;Cbe代表从b系到e系的转换矩阵。其他变量的上标表示投影坐标系,下标表示参考坐标系或目标坐标系。以ωebe为例,上下标表示b系相对于e系的旋转角速度向量在e系中的投影[3]。由于初始状态和IMU观测值存在误差,以及重力存在偏差,导致INS递推算法的误差随着时间快速累积。限于篇幅原因,直接给出e系下INS误差方程[4, 14-15]
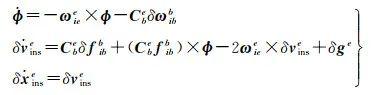 (2)
(2)
式中,ϕ代表Phi角模型[4]下的姿态误差;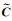
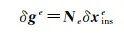
式中

式中,r是从地心地固系的原点到xbe的几何距离;GM是地球引力常数[4, 17-18]。角速度和比力的测量误差表示为[4, 14-15]
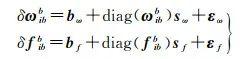 (3)
(3)
式中,bω、bf、sω、sf、εω和εf分别表示陀螺仪和加表的残余零偏项、比例因子项和量测噪声。由于IMU每次上电后的残余零偏项和比例因子项都不尽相同,因此无法通过先验校正,而需要通过参数估计的方式对其进行补偿。通常对残余零偏项和比例因子项建立一阶马尔可夫过程[4]
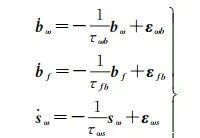 (4)
(4)
式中,τωb、τfb、τωs、τfs和εωb、εfb、εωs、εfs分别表示相应变量的相关时间和驱动白噪声,其数值由IMU自身性能决定。至此,INS的待估参数向量为δxins= [ϕ, δ vbe, δxbe, bω, bf, sω, sf]T,其时间更新方程为
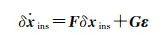 (5)
(5)
式中
 (6)
(6)
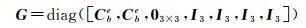 (7)
(7)
在GNSS相对定位中,短基线双差载波相位和伪距观测方程为[19-23]
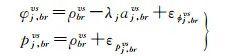 (8)
(8)
式中,φ、p分别为载波相位和伪距观测值;ρ、λ、a、ε分别表示卫地距、波长、双差模糊度和观测噪声。下标j、b、r分别表示频率、基准站与流动站;上标v、s代表来自同一卫星系统的两颗卫星;(*)brvs=(*)rs-(*)rv-(*)bs+(*)bv为双差算子;本文以单频双模为例给出单历元向量形式的GNSS观测方程,多频多模GNSS观测方程可通过类似的方式推导得到。假设分别观测到来自卫星系统Q和K的n颗和m颗卫星,则单历元GNSS观测方程的函数模型和随机模型分别为
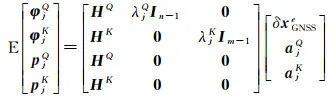 (9)
(9)
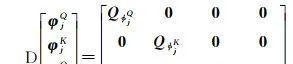 (10)
(10)
式中,H代表坐标向量的设计矩阵[17];δxGNSSe代表相对于GNSS天线相位中心的坐标改正值;QϕjQ、QϕjK、QpjQ、QpjK分别为双差载波相位和伪距观测值对应的方差-协方差矩阵,本文采用文献[24]的信号载噪比定权。
GNSS/INS组合在算法层面上包括松组合和紧组合两种方式。松组合是结果层面上的组合,要求至少同时观测到4颗卫星;而紧组合是观测值层面的组合,即使卫星数小于4颗也可进行组合解算[25]。考虑到复杂环境中观测卫星数不足4颗的情况时常发生,导致松组合频繁失效,因此本文将采用GNSS/INS紧组合进行公式推导。
GNSS观测值在GNSS/INS组合导航中起到量测更新的作用,因此组合导航算法的核心是建立INS误差与GNSS观测值的数学关系。由于IMU中心与GNSS天线相位中心不重合,二者之间存在一个在b系中维持恒定的距离,称之为杆臂l,如图 1所示。
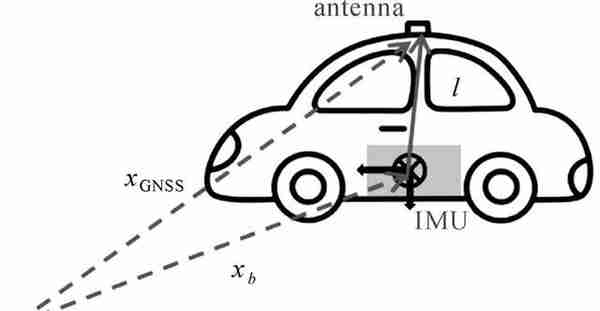 |
| 图 1 GNSS天线相位中心与IMU中心空间关系Fig. 1 The spatial relationship between GNSS antenna phase center and IMU center |
图选项 |
根据空间向量关系,在e系中有
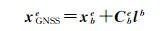 (11)
(11)
对其进行误差扰动,得到e系下的GNSS天线相位中心的坐标误差与IMU中心的坐标误差之间的关系
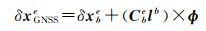 (12)
(12)
联合式(5)、式(9)和式(12),并顾及GNSS和INS对误差定义相反[13, 15],得GNSS/INS紧组合的观测方程为
 (13)
(13)
将式(13)简写为E[y]= Ax,其中,x = 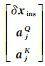
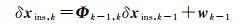 (14)
(14)
式中,转移矩阵Φk-1, k≈ I + Fk-1Δt,噪声wk-1的方差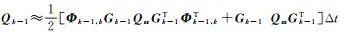
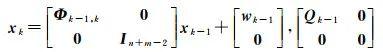 (15)
(15)
1.2 多车协同定位数学模型
本文以4辆车的情形为例阐述多车协同定位方法,多车之间的协同定位原理类似,如图 2所示。
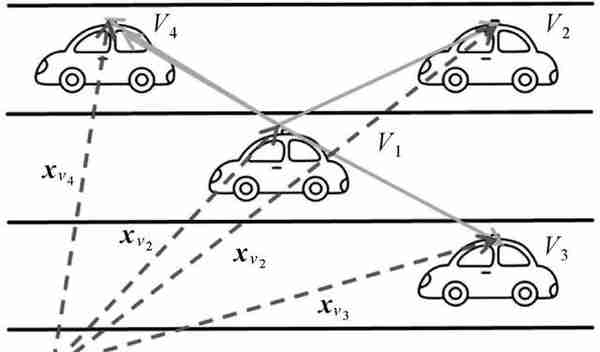 |
| 图 2 多车协同定位Fig. 2 Multi-vehicle cooperative positioning |
图选项 |
假设事先采用某种方式确定了载体V1、V2、V3之间的相对空间关系d12、d13、d23(可通过GNSS相对定位、视觉/激光雷达匹配等技术得到),以GNSS相对定位为例,此时可以直接得到e系下两辆车之间的相对空间距离de= Cvedv,其中v代表车辆坐标系,Cve可从组合导航程序得到。注意,下文讨论均以载体的IMU中心为坐标参考点,且IMU安装时与车辆的轴向严格对齐。根据式(12),可以得到
 (16)
(16)
此时车辆之间的量测更新方程为
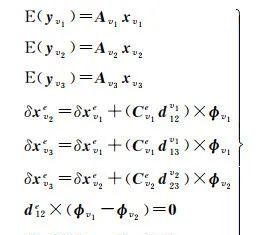 (17)
(17)
量测方程的随机模型为
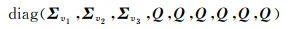 (18)
(18)
式中,Σv1、Σv2、Σv3表示3辆车的GNSS观测向量的方差-协方差矩阵,其形式类似于式(10)。Q=σ2I3表示每个约束式(16)的随机模型,σ反映了约束式(16)的先验精度,根据经验其取值范围为0.05~0.1 m。结合式(17)可以看到,协同定位模式相比于单独解算模式增加了更多的约束,相当于将这3辆车视为一个整体,从而不仅实现各辆车之间的观测值共享,也大大增加了观测冗余,提高了定位质量。
2.1 试验设计
为了验证提出算法的有效性,本文开展了一组半仿真双车协同定位试验。试验数据于2021年7月13日在同济大学校园内采集,测试环境较为开阔,试验测试轨迹如图 3所示。两辆小车(记为VA、VB)分别用于采集各自的导航数据(GNSS和IMU观测值)。VA上搭载了型号为Sepetentrio asterX-D的GNSS/INS组合设备,其中,GNSS采样率为1 Hz,内置IMU型号为ADIS16505,且采样率为100 Hz;VB上搭载了Xsens MTIG710和Trimble Alloy,其中IMU采样率为100 Hz,Alloy的采样频率为1 Hz。MTIG710和ADIS16505的参数见表 1。基准站为Trimble Alloy接收机,架设在300 m以内的测绘馆楼顶,采样频率为1 Hz。需要注意的是,IMU说明手册上提供的参数通常代表产品在理想环境下的指标,实际应用环境中可能会偏优,用户可根据实际情况对参数进行优化。
 |
| 图 3 测试路线与设备安装Fig. 3 Test route and equipment installation |
图选项 |
表 1 MTIG710和ADIS16505设备参数*Tab. 1 The equipment parameters of MTIG710 and ADIS16505
| IMU型号 | 陀螺零偏稳定性/((°)/h) | 陀螺角度随机游走/((°)/sqrt(h)) | ug | 加表速度随机游走/(ug/sqrt(h)) |
| MTIG710 | 10 | 0.6 | 15 | 0.036 |
| ADIS16505 | 2.7 | 0.2 | 4.4 | 0.015 |
| *注:参数源自MTIG710(https://www.xsens.com/mti-g-710)与asterX-D(https://www.septentrio.com/zh-hans/chanpin/gnssjieshouji/gnss-oembanka/asterx-i3-d-pro)说明手册。 | ||||
表选项
实现协同精密定位的前提是精确确定车辆之间的相对空间关系,这也是协同定位的核心和难点,特别是当车辆处于复杂的高遮挡环境中时,如何结合车辆之间的多传感器实现高精度的空间相对位置确定依然是未来研究关注点。本文旨在验证协同定位思想的效果,本文试验中VA和VB的相对位置关系将通过动对动RTK事先计算得到,两辆车之间的空间位置变化如图 4所示。为了对比协同技术在不同环境下对定位的改善效果,通过控制双差观测值个数来模拟不同条件的观测环境。
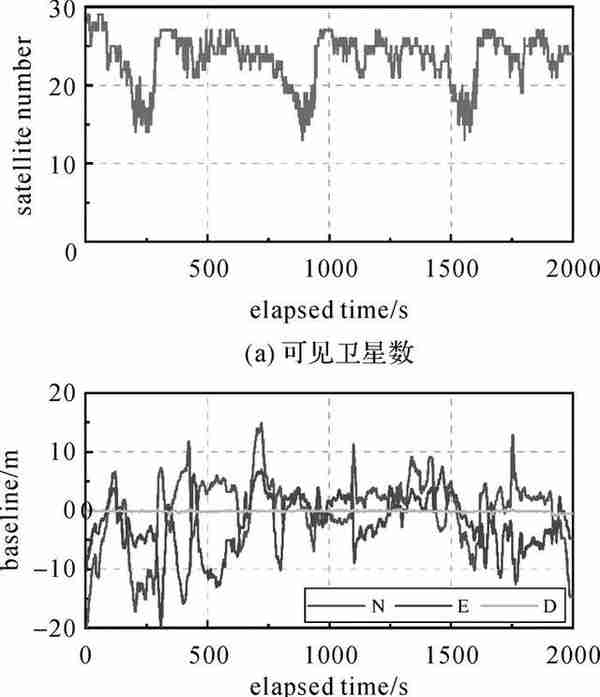 |
| 图 4 可见卫星数及VA和VB间基线变化情况Fig. 4 The number of visible satellites and the baseline between VA and VB |
图选项 |
(1) T1(1~500 s):不改变VA和VB的双差观测值个数。
(2) T2(501~1000 s):保留VB高度角最高的3对双差观测值,不改变VA的双差观测值个数。
(3) T3(1001~1500 s):保留VA和VB高度角最高的3对双差观测值。
(4) T4(1501~2000 s):不改变VA的双差观测值个数,为了测试在单载体卫星信号完全失锁情况下的协同定位性能,在此时段末端20 s内丢弃VB所有的双差观测值,其余时段不改变VB的双差观测值个数。
另外,将VA和VB在正常观测环境下GNSS/INS双向平滑的紧组合结果作为各自轨迹的参考值。
2.2 结果与分析
图 5给出了VA和VB在独立模式和协同模式下的位置误差序列,图 6展示了三维位置误差累积分布函数(cumulative distribution function,CDF)。表 2和表 3给出了相应的精度统计结果。图 7和8展示了VA和VB在独立模式和协同模式下的速度与姿态误差序列。
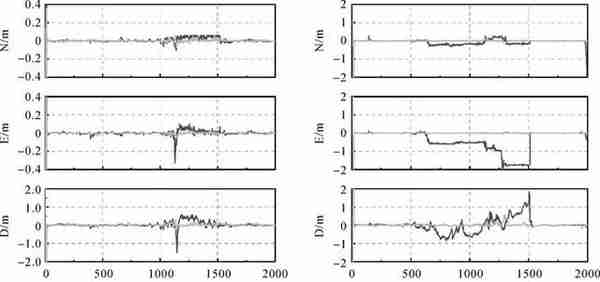 |
| 图 5 位置误差时间序列 Fig. 5 The position error series |
图选项 |
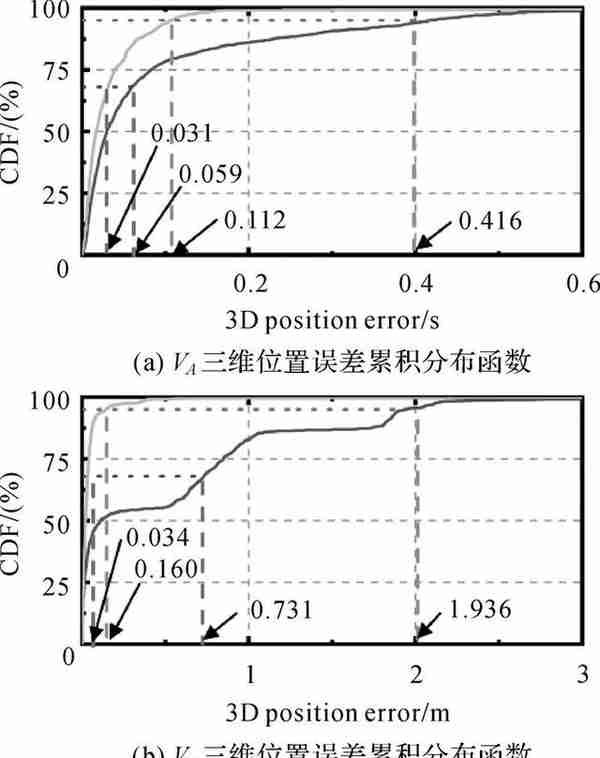 |
| 图 6 三维位置误差累积分布函数 Fig. 6 CDF of 3D position error series |
图选项 |
表 2 不同时段内VA定位误差统计信息 Tab. 2 The statistics of each period 3D positioning error of VA
| 时段 | RMS | 68% | 95% | |||||
| 独立定位 | 协同定位 | 独立定位 | 协同定位 | 独立定位 | 协同定位 | |||
| T1 | 0.041 | 0.025 | 0.045 | 0.023 | 0.121 | 0.075 | ||
| T2 | 0.039 | 0.027 | 0.029 | 0.020 | 0.094 | 0.051 | ||
| T3 | 0.329 | 0.073 | 0.339 | 0.067 | 0.534 | 0.142 | ||
| T4 | 0.036 | 0.037 | 0.027 | 0.021 | 0.082 | 0.094 | ||
| 合计 | 0.169 | 0.045 | 0.059 | 0.031 | 0.416 | 0.112 | ||
表选项
表 3 不同时段内VB定位误差统计信息 Tab. 3 The statistics of each period 3D positioning error of VB
| 时段 | RMS | 68% | 95% | |||||
| 独立定位 | 协同定位 | 独立定位 | 协同定位 | 独立定位 | 协同定位 | |||
| T1 | 0.044 | 0.028 | 0.041 | 0.029 | 0.116 | 0.079 | ||
| T2 | 0.651 | 0.032 | 0.777 | 0.033 | 0.970 | 0.073 | ||
| T3 | 1.435 | 0.130 | 1.838 | 0.059 | 2.117 | 0.367 | ||
| T4 | 0.684 | 0.030 | 0.015 | 0.021 | 1.829 | 0.059 | ||
| 合计 | 0.864 | 0.071 | 0.859 | 0.034 | 2.792 | 0.160 | ||
表选项
 |
| 图 7 速度误差时间序列 Fig. 7 The velocity error series |
图选项 |
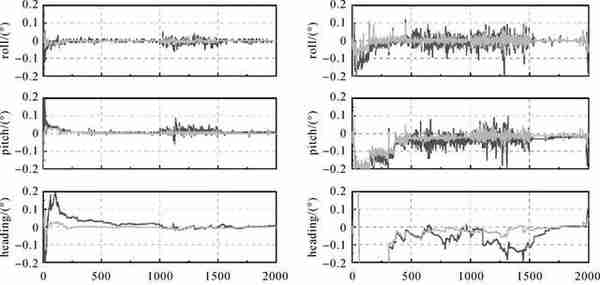 |
| 图 8 姿态误差时间序列 Fig. 8 The velocity error series |
图选项 |
由整体试验结果可知,协同定位的精度显著优于载体独立定位效果,VA和VB独立定位的RMS分别为0.169和0.864 m,协同定位的RMS分别为0.045和0.071 m,精度提升了73.37%和91.78%;VA和VB独立定位68%对应的CDF分别为0.059和0.859 m,协同模式下该指标分别为0.031和0.034 m,提升了47.46%和96.04%;95%对应的CDF分别从0.416、2.792 m提升至0.112、0.160 m,分别得到了73.87%和94.27%的改善。
从不同环境下的结果看,当载体在较为开阔的环境中运动时(T1和T4前段),无论是单独导航解算还是协同定位,VA与VB均取得了较高的定位精度,三维定位精度均达到厘米级。因为在开阔环境下,即使基于载体本身传感器的定位,也能观测到足够数量的GNSS卫星,能够有效抑制INS误差的累积。但当载体在可用GNSS观测值较少的环境中运动时(T2、T3和T4最后20 s),独立模式下的定位误差会随着时间增加而快速累积,其累积速度取决于IMU设备的精度与在恶劣环境中的运动时长。而采用了协同定位模式后,两辆车在此环境下的定位精度均得到了显著提高。对于VA而言,当采用单独导航模式时,在T3时段内三维定位的RMS、CDF(68%)和CDF(95%)对应的误差分别为0.329、0.339和0.534 m,而当采用协同定位模式时,3个统计量降至0.073、0.067和0.142 m,提升了77.81%、80.24%和73.41%。以VB定位效果改善最为明显的T3时段为例,当采用单独导航模式时,三维定位误差的RMS、CDF(68%)和CDF(95%)对应的误差分别为1.435、1.838和2.117 m,当采用协同定位模式时,3个统计量降至0.130、0.059和0.367 m,提升百分比分别为90.94%、96.79%和82.66%。
本文结合图 7和图 8简要分析协同与独立模式在测速与定姿精度上的差异。当可用GNSS观测值较多时,无论是VA还是VB,协同与独立模式最终都取得了相当的测速与定姿精度。此外,观察VA的T1时段与VB的T4时段,可以发现协同相比于独立模式明显缩短了速度与姿态的收敛时间;当载体在可用GNSS观测值较少的环境中运动并且采用独立模式时,无论是VA还是VB,其速度与姿态精度都会有不同程度的发散,发散的速度取决于IMU器件的精度。而当采用协同定位模式时,VA与VB即使在恶劣环境中也能保持非常高的测速与定姿精度。这说明协同模式不仅可以改善车辆的定位精度,也可以有效改善车辆的测速与定姿精度,并且加快待估参数的收敛速度。
以上结果表明在复杂环境下,独立载体即使采用GNSS/INS组合方式也会导致定位、测速与定姿结果发散,其根本原因是观测卫星数有限导致长时间无法提供外部绝对辅助信息从而无法抑制INS误差。而协同定位技术通过共享车辆之间的观测值,在车辆之间建立相对位置约束关系,有效增加载体可用观测量以抑制INS误差的发散。此外,一旦车辆间的相对位置实现高精度协同,多载体就会被固连为一个刚体,此时相当于一个载体上搭载了多台多元传感器设备,能有效提高定位的可信度。需要说明的是,由于试验硬件有限,尽管本文仅采用了两辆车验证协同定位效果,但多车协同的实现过程是类似的,因此不妨碍对本文算法可行性的验证。当然,参与协同的车辆越多,单个车辆能够利用的观测值便越多,越有利于提高协同定位的效果。
本文基于目前最常用的GNSS/INS组合导航技术,推导了GNSS/INS多车协同紧组合定位模型和解算方法,通过建立车辆之间的相对位置关系,实现车辆之间的信息共享,从而提升多车定位精度。通过设计双车协同定位试验,模拟不同复杂观测环境,对比分析了协同定位模式相比于单独导航模式在定位、测速与定姿精度方面的差异。结果表明,协同定位模式能显著改善载体在复杂环境下的定位精度,两辆车的独立定位RMS分别被提升了73.37%和91.78%,同时也能够改善测速与定姿的精度并加快参数的收敛速度。本文可为后续深化协同定位技术在智慧交通和无人驾驶领域中的应用抛砖引玉。
第一作者简介:李博峰(1983—),男,博士,教授,研究方向为卫星大地测量。E-mail:bofeng_li@tongji.edu.cn






